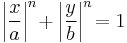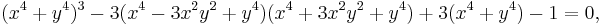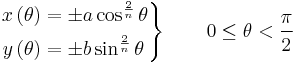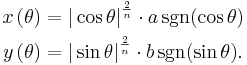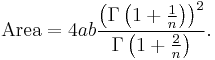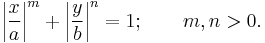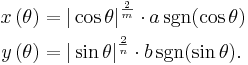Superellipse

A superellipse (or Lamé curve) is a geometric figure defined in the Cartesian coordinate system as the set of all points (x, y) with

\left|\frac{x}{a}\right|^n\! %2B \left|\frac{y}{b}\right|^n\! = 1

where n, a and b are positive numbers.

This formula defines a closed curve contained in the rectangle −a ≤ x ≤ +a and −b ≤ y ≤ +b. The parameters a and b are called the semi-diameters of the curve.

When n is between 0 and 1, the superellipse looks like a four-armed star with concave (inwards-curved) sides. For n = 1/2, in particular, the sides are arcs of parabolas.

When n is 1 the curve is a diamond with corners (±a, 0) and (0, ±b). When n is between 1 and 2, it looks like a diamond with those same corners but with convex (outwards-curved) sides. The curvature increases without limit as one approaches the corners.

When n is 2, the curve is an ordinary ellipse (in particular, a circle if a = b). When n is greater than 2, it looks superficially like a rectangle with chamfered (rounded) corners. The curvature is zero at the points (±a, 0) and (0, ±b).

If n < 2, the figure is also called a hypoellipse; if n > 2, a hyperellipse.

When n ≥ 1 and a = b, the superellipse is the boundary of a ball of R2 in the n-norm.

The extreme points of the superellipse are (±a, 0) and (0, ±b), and its four "corners" are (±sa, ±sb), where 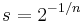s=2^{-1/n} (sometimes called the "superness" [1]).

Contents

Algebraic properties

When n is a nonzero rational number p / q (in lowest terms), then the superellipse is a plane algebraic curve. For positive n the order is pq; for negative n the order is 2pq. In particular, when a and b are both one and n is an even integer, then it is a Fermat curve of degree n. In that case it is nonsingular, but in general it will be singular. If the numerator is not even, then the curve is pasted together from portions of the same algebraic curve in different orientations.

For example, if x4/3 + y4/3 = 1, then the curve is an algebraic curve of degree twelve and genus three, given by the implicit equation

(x^4%2By^4)^3-3(x^4-3x^2y^2%2By^4)(x^4%2B3x^2y^2%2By^4)%2B3(x^4%2By^4)-1=0 , \,\!

or by the parametric equations

\left. \begin{align} x\left(\theta\right) &= \plusmn a\cos^{\frac{2}{n}} \theta \\ y\left(\theta\right) &= \plusmn b\sin^{\frac{2}{n}} \theta \end{align} \right\} \qquad 0 \le \theta < \frac{\pi}{2}

or

\begin{align} x\left(\theta\right) &= {|\cos \theta|}^{\frac{2}{n}} \cdot a \sgn(\cos \theta) \\ y\left(\theta\right) &= {|\sin \theta|}^{\frac{2}{n}} \cdot b \sgn(\sin \theta). \end{align}

The area inside the superellipse can be expressed in terms of the gamma function, Γ(x), as

\mathrm{Area} = 4 a b \frac{\left(\Gamma \left(1%2B\tfrac{1}{n}\right)\right)^2}{\Gamma \left(1%2B\tfrac{2}{n}\right)} .

Generalizations

The superellipse is further generalized as:

\left|\frac{x}{a}\right|^m %2B \left|\frac{y}{b}\right|^n = 1; \qquad m, n > 0.

or

\begin{align} x\left(\theta\right) &= {|\cos \theta|}^{\frac{2}{m}} \cdot a \sgn(\cos \theta) \\ y\left(\theta\right) &= {|\sin \theta|}^{\frac{2}{n}} \cdot b \sgn(\sin \theta). \end{align}

(Note that :\theta is NOT a physical angle of the figure, but just a parameter)

History

The general Cartesian notation of the form comes from the French mathematician Gabriel Lamé (1795–1870) who generalized the equation for the ellipse.

Though he is often credited with its invention, the Danish poet and scientist Piet Hein (1905–1996) did not discover the super-ellipse. In 1959, city planners in Stockholm, Sweden announced a design challenge for a roundabout in their city square Sergels Torg. Piet Hein's winning proposal was based on a superellipse with n = 2.5 and a/b = 6/5.[2] As he explained it:

Man is the animal that draws lines which he himself then stumbles over. In the whole pattern of civilization there have been two tendencies, one toward straight lines and rectangular patterns and one toward circular lines. There are reasons, mechanical and psychological, for both tendencies. Things made with straight lines fit well together and save space. And we can move easily — physically or mentally — around things made with round lines. But we are in a straitjacket, having to accept one or the other, when often some intermediate form would be better. To draw something freehand — such as the patchwork traffic circle they tried in Stockholm — will not do. It isn't fixed, isn't definite like a circle or square. You don't know what it is. It isn't esthetically satisfying. The super-ellipse solved the problem. It is neither round nor rectangular, but in between. Yet it is fixed, it is definite — it has a unity.

Sergels Torg was completed in 1967. Meanwhile Piet Hein went on to use the superellipse in other artifacts, such as beds, dishes, tables, etc.[3] By rotating a superellipse around the longest axis, he created the superegg, a solid egg-like shape that could stand upright on a flat surface, and was marketed as a novelty toy.

In 1968, when negotiators in Paris for the Vietnam War could not agree on the shape of the negotiating table, Balinski, Kieron Underwood and Holt suggested a superelliptical table in a letter to the New York Times.[2] The superellipse was used for the shape of the 1968 Azteca Olympic Stadium, in Mexico City.

Waldo R. Tobler developed a map projection, the Tobler hyperelliptical projection, published in 1973,[4] in which the meridians are arcs of superellipses.

Hermann Zapf's typeface Melior, published in 1952, uses superellipses for letters such as o. Many web sites say Zapf actually drew the shapes of Melior by hand without knowing the mathematical concept of the superellipse, and only later did Piet Hein point out to Zapf that his curves were extremely similar to the mathematical construct, but these web sites do not cite any primary source of this account. Thirty years later Donald Knuth built into his Computer Modern type family the ability to choose between true ellipses and superellipses (both approximated by cubic splines).

Three connected superellipses are used in the logo of the Pittsburgh Steelers.

See also

References

  1. ^ Donald Knuth: The METAFONTbook, p. 126
  2. ^ a b Gardner, Martin (1977), "Piet Hein’s Superellipse", Mathematical Carnival. A New Round-Up of Tantalizers and Puzzles from Scientific American, New York: Vintage Press, pp. 240–254, ISBN 978-0-394-72349-5 
  3. ^ The Superellipse, in The Guide to Life, The Universe and Everything by BBC (27th June 2003)
  4. ^ Tobler, Waldo (1973), "The hyperelliptical and other new pseudocylindrical equal area map projections", Journal of Geophysical Research 78 (11): 1753–1759, Bibcode 1973JGR....78.1753T, doi:10.1029/JB078i011p01753. 

External links